2
| Input | Output | ||
| \(x_0\) | \(y_0\) | \(c_0\) | \(s_0\) |
| \(1\) | \(1\) | ||
| \(1\) | \(0\) | ||
| \(0\) | \(1\) | ||
| \(0\) | \(0\) | ||
We have the following subset relationships between sets of numbers:
\[\mathbb{Z}^{+} \subsetneq \mathbb{N} \subsetneq \mathbb{Z} \subsetneq \mathbb{Q} \subsetneq \mathbb{R}\]
Which of the proper subset inclusions above can you prove?
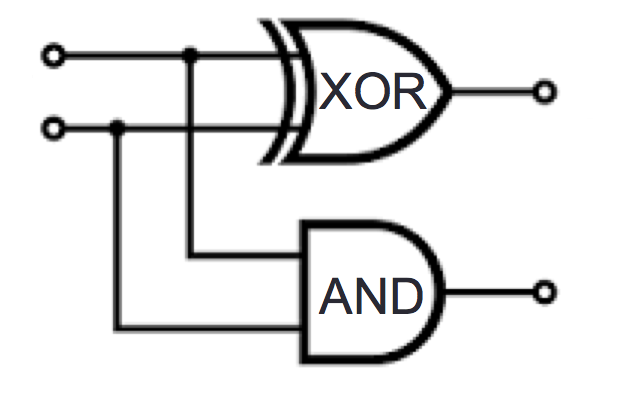
Fixed-width addition: adding one bit at time, using the usual column-by-column and carry arithmetic, and dropping the carry from the leftmost column so the result is the same width as the summands. In many cases, this gives representation of the correct value for the sum when we interpret the summands in fixed-width binary or in 2s complement.
For single column:
2
| Input | Output | ||
| \(x_0\) | \(y_0\) | \(c_0\) | \(s_0\) |
| \(1\) | \(1\) | ||
| \(1\) | \(0\) | ||
| \(0\) | \(1\) | ||
| \(0\) | \(0\) | ||

Draw a logic circuit that implements binary addition of two numbers that are each represented in fixed-width binary:
Inputs \(x_0, y_0, x_1, y_1\) represent \((x_1 x_0)_{2,2}\) and \((y_1 y_0)_{2,2}\)
Outputs \(z_0, z_1, z_2\) represent \((z_2 z_1 z_0)_{2,3} = (x_1 x_0)_{2,2} + (y_1 y_0)_{2,2}\) (may require up to width \(3\))
First approach: half-adder for each column, then combine carry from right column with sum of left column
Write expressions for the circuit output values in terms of input values:
\(z_0 = \underline{\phantom{x_0 \oplus y_0\hspace{3in}}}\)
\(z_1 = \underline{\phantom{(x_1 \oplus y_1) \oplus c_0}\hspace{2.5in}}\)
\(z_2 = \underline{\phantom{(c_0 \land (x_1
\oplus y_1)) \oplus c_1}\hspace{2in}}\)
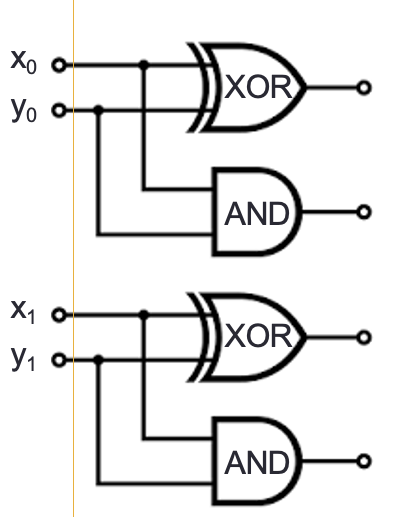
There are other approaches, for example: for middle column, first add carry from right column to \(x_1\), then add result to \(y_1\)
Let’s practice with functions related to some of our applications so far.
Recall: We model the collection of user ratings of the four movies Superman, Wicked, KPop Demon Hunters, A Minecraft Movie as the set \(\{-1,0,1\}^4\) . One function that compares pairs of ratings is \[d_0: \{-1,0,1\}^4 \times \{-1,0,1\}^4 \to \mathbb{R}\] given by \[d_0 (~(~ (x_1, x_2, x_3, x_4), (y_1, y_2, y_3, y_4) ~) ~) = \sqrt{ (x_1 - y_1)^2 + (x_2 - y_2)^2 + (x_3 -y_3)^2 + (x_4 -y_4)^2}\]
Notice: any ordered pair of ratings is an okay input to \(d_0\).
Notice: there are (at most) \[(3 \cdot 3 \cdot 3 \cdot 3)\cdot (3 \cdot 3 \cdot 3 \cdot 3) = 3^8 = 6561\] many pairs of ratings. There are therefore lots and lots of real numbers that are not the output of \(d_0\).
Recall: RNA is made up of strands of four different bases that encode
genomic information in specific ways.
The bases are elements of the set \(B =
\{\texttt{A}, \texttt{C}, \texttt{U}, \texttt{G}\}\). The set of
RNA strands \(S\) is defined
(recursively) by: \[\begin{array}{ll}
\textrm{Basis Step: } & \texttt{A}\in S, \texttt{C}\in S,
\texttt{U}\in S, \texttt{G}\in S \\
\textrm{Recursive Step: } & \textrm{If } s \in S\textrm{ and }b \in
B \textrm{, then }sb \in S
\end{array}\] where \(sb\) is
string concatenation.
Pro-tip: informal definitions sometime use \(\cdots\) to indicate “continue the pattern”. Often, to make this pattern precise we use recursive definitions.
| Name | Domain | Codomain | Rule | Example |
|---|---|---|---|---|
| \(rnalen\) | \(S\) | \(\mathbb{Z}^+\) | \[\begin{align*} &\textrm{Basis Step:} \\ &\textrm{If } b \in B\textrm{ then } \textit{rnalen}(b) = 1 \\ &\textrm{Recursive Step:}\\ &\textrm{If } s \in S\textrm{ and } b \in B\textrm{, then }\\ &\textit{rnalen}(sb) = 1 + \textit{rnalen}(s) \end{align*}\] | \[\begin{align*} rnalen(\texttt{A}\texttt{C}) &\overset{\text{rec step}}{=} 1 +rnalen(\texttt{A}) \\ &\overset{\text{basis step}}{=} 1 + 1 = 2 \end{align*}\] |
| \(basecount\) | \(S \times B\) | \(\mathbb{N}\) | \[\begin{align*} &\textrm{Basis Step:} \\ &\textrm{If } b_1 \in B, b_2 \in B \textrm{ then} \\ &basecount(~(b_1, b_2)~) = \\ &\begin{cases} 1 & \textrm{when } b_1 = b_2 \\ 0 & \textrm{when } b_1 \neq b_2 \\ \end{cases}\\ &\textrm{Recursive Step:}\\ &\textrm{If } s \in S, b_1 \in B, b_2 \in B\\ &basecount(~(sb_1, b_2)~) = \\ &\begin{cases} 1 + \textit{basecount}(~(s, b_2)~) & \textrm{when } b_1 = b_2 \\ \textit{basecount}(~(s, b_2)~) & \textrm{when } b_1 \neq b_2 \\ \end{cases} \end{align*}\] | \[\begin{align*} basecount(~(\texttt{A}\texttt{C}\texttt{U}, \texttt{C})~) = \end{align*}\] |
| “\(2\) to the power of” | \(\mathbb{N}\) | \(\mathbb{N}\) | \[\begin{align*} &\textrm{Basis Step:} \\ &2^0= 1 \\ &\textrm{Recursive Step:}\\ &\textrm{If } n \in \mathbb{N}, 2^{n+1} = \phantom{2 \cdot 2^n} \end{align*}\] | |
| “\(b\) to the power of \(i\)” | \(\mathbb{Z}^+ \times \mathbb{N}\) | \(\mathbb{N}\) | \[\begin{align*} &\textrm{Basis Step:} \\ &b^0 = 1 \\ &\textrm{Recursive Step:}\\ &\textrm{If } i \in \mathbb{N}, b^{i+1} = b \cdot b^i \end{align*}\] |
Integer division and remainders (aka The Division Algorithm) Let \(n\) be an integer and \(d\) a positive integer. There are unique integers \(q\) and \(r\), with \(0 \leq r < d\), such that \(n = dq + r\). In this case, \(d\) is called the divisor, \(n\) is called the dividend, \(q\) is called the quotient, and \(r\) is called the remainder.
Because these numbers are guaranteed to exist, the following functions are well-defined:
\(\textbf{ div } : \mathbb{Z} \times \mathbb{Z}^+ \to \mathbb{Z}\) given by \(\textbf{ div } ( ~(n,d)~)\) is the quotient when \(n\) is the dividend and \(d\) is the divisor.
\(\textbf{ mod } : \mathbb{Z} \times \mathbb{Z}^+ \to \mathbb{Z}\) given by \(\textbf{ mod } ( ~(n,d)~)\) is the remainder when \(n\) is the dividend and \(d\) is the divisor.
Because these functions are so important, we sometimes use the notation \(n \textbf{ div } d = \textbf{ div } ( ~(n,d)~)\) and \(n \textbf{ mod } d = \textbf{ mod } (~(n,d)~)\).
Pro-tip: The functions \(\textbf{ div }\) and \(\textbf{ mod }\) are similar to (but not exactly the same as) the operators \(/\) and \(\%\) in Java and python.
Example calculations:
\(20 \textbf{ div } 4\)
\(20 \textbf{ mod } 4\)
\(20 \textbf{ div } 3\)
\(20 \textbf{ mod } 3\)
\(-20 \textbf{ div } 3\)
\(-20 \textbf{ mod } 3\)
Modeling uses data-types that are encoded in a computer. The details of the encoding impact the efficiency of algorithms we use to understand the systems we are modeling and the impacts of these algorithms on the people using the systems. Case study: how to encode numbers?
Definition For \(b\) an integer greater than \(1\) and \(n\) a positive integer, the base \(b\) expansion of \(n\) is \[(a_{k-1} \cdots a_1 a_0)_b\] where \(k\) is a positive integer, \(a_0, a_1, \ldots, a_{k-1}\) are (symbols for) nonnegative integers less than \(b\), \(a_{k-1} \neq 0\), and \[n = \sum_{i=0}^{k-1} a_{i} b^{i}\]
Notice: The base \(b\) expansion of a positive integer \(n\) is a string over the alphabet \(\{x \in \mathbb{N} \mid x < b\}\) whose leftmost character is nonzero.
| Base \(b\) | Collection of possible coefficients in base \(b\) expansion of a positive integer |
|---|---|
| Binary (\(b=2\)) | \(\{0,1\}\) |
| Ternary (\(b=3\)) | \(\{0,1, 2\}\) |
| Octal (\(b=8\)) | \(\{0,1, 2, 3, 4, 5, 6, 7\}\) |
| Decimal (\(b=10\)) | \(\{0,1, 2, 3, 4, 5, 6, 7, 8, 9\}\) |
| Hexadecimal (\(b=16\)) | \(\{0,1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F\}\) |
| letter coefficient symbols represent numerical values \((A)_{16} = (10)_{10}\) | |
| \((B)_{16} = (11)_{10} ~~(C)_{16} = (12)_{10} ~~ (D)_{16} = (13)_{10} ~~ (E)_{16} = (14)_{10} ~~ (F)_{16} = (15)_{10}\) |
Examples:
\((1401)_{2}\)
\((1401)_{10}\)
\((1401)_{16}\)
Algorithms can be expressed in English or in more formalized descriptions like pseudocode or fully executable programs.
Sometimes, we can define algorithms whose output matches the rule for a function we already care about. Consider the (integer) logarithm function \[logb : \{b \in \mathbb{Z} \mid b >1 \} \times \mathbb{Z}^+ ~~\to~~ \mathbb{N}\] defined by \[logb (~ (b,n)~) = \text{greatest integer } y \text{ so that } b^y \text{ is less than or equal to } n\]
procedure \(logb\)(\(b\),\(n\): positive integers with \(b > 1\)) \(i\) := \(0\) while \(n\) > \(b-1\) \(i\) := \(i + 1\) \(n\) := \(n\) div \(b\) return \(i\) \(\{ i\) holds the integer part of the base \(b\) logarithm of \(n\}\)
Trace this algorithm with inputs \(b=3\) and \(n=17\)
| \(b\) | \(n\) | \(i\) | \(n > b-1\)? | |
|---|---|---|---|---|
| Initial value | \(3\) | \(17\) | ||
| After 1 iteration | ||||
| After 2 iterations | ||||
| After 3 iterations | ||||
Compare: does the output match the rule for the (integer) logarithm function?
Two algorithms for constructing base \(b\) expansion from decimal representation
Most significant first: Start with left-most coefficient of expansion (highest value)
Informally: Build up to the value we need to represent in “greedy” approach, using units determined by base.
procedure \(\textit{basebmost}\)(\(n, b\): positive integers with \(b > 1\)) \(v\) := \(n\) \(k\) := \(1 +\) output of \(logb\) algorithm with inputs \(b\) and \(n\) for \(i\) := \(1\) to \(k\) \(a_{k-i}\) := \(0\) while \(v \geq b^{k-i}\) \(a_{k-i}\) := \(a_{k-i} + 1\) \(v\) := \(v - b^{k-i}\) return \((a_{k-1}, \ldots, a_0) \{(a_{k-1} \ldots a_0)_b~\textrm{ is the base } b \textrm{ expansion of } n \}\)
Least significant first: Start with right-most coefficient of expansion (lowest value)
Idea: (when \(k > 1\)) \[\begin{align*} n &= a_{k-1} b^{k-1} + \cdots + a_1 b + a_0 \\ &= b ( a_{k-1} b^{k-2} + \cdots + a_1) + a_0 \end{align*}\] so \(a_0 = n \textbf{ mod } b\) and \(a_{k-1} b^{k-2} + \cdots + a_1 = n \textbf{ div } b\).
procedure \(\textit{basebmost}\)(\(n, b\): positive integers with \(b > 1\)) \(v\) := \(n\) \(k\) := \(1 +\) output of \(logb\) algorithm with inputs \(b\) and \(n\) for \(i\) := \(1\) to \(k\) \(a_{k-i}\) := \(0\) while \(v \geq b^{k-i}\) \(a_{k-i}\) := \(a_{k-i} + 1\) \(v\) := \(v - b^{k-i}\) return \((a_{k-1}, \ldots, a_0) \{(a_{k-1} \ldots a_0)_b~\textrm{ is the base } b \textrm{ expansion of } n \}\)
Find and fix any and all mistakes with the following:
\((1)_2 = (1)_8\)
\((142)_{10} = (142)_{16}\)
\((20)_{10} = (10100)_2\)
\((35)_8 = (1D)_{16}\)
Practice: write an algorithm for converting from base \(b_1\) expansion to base \(b_2\) expansion:
To define sets:
To define a set using roster method, explicitly list its elements. That is, start with \(\{\) then list elements of the set separated by commas and close with \(\}\).
To define a set using set builder definition, either form “The set of all \(x\) from the universe \(U\) such that \(x\) is ..." by writing \[\{x \in U \mid ...x... \}\] or form “the collection of all outputs of some operation when the input ranges over the universe \(U\)" by writing \[\{ ...x... \mid x\in U \}\]
We use the symbol \(\in\) as “is an
element of” to indicate membership in a set.
Example sets: For each of the following, identify whether it’s defined using the roster method or set builder notation and give an example element.
Can we infer the data type of the example element from the notation?
\(\{ -1, 1\}\)
\(\{0, 0 \}\)
\(\{-1, 0, 1 \}\)
\(\{(x,x,x) \mid x \in \{-1,0,1\} \}\)
\(\{ \}\)
\(\{ x \in \mathbb{Z} \mid x \geq 0 \}\)
\(\{ x \in \mathbb{Z} \mid x > 0 \}\)
\(\{ \smile, \sun \}\)
\(\{\texttt{A},\texttt{C},\texttt{U},\texttt{G}\}\)
\(\{\texttt{A}\texttt{U}\texttt{G}, \texttt{U}\texttt{A}\texttt{G}, \texttt{U}\texttt{G}\texttt{A}, \texttt{U}\texttt{A}\texttt{A}\}\)
RNA is made up of strands of four different bases that encode genomic
information in specific ways.
The bases are elements of the set \(B =
\{\texttt{A}, \texttt{C}, \texttt{U}, \texttt{G}\}\). Strands are
ordered nonempty finite sequences of bases.
Formally, to define the set of all RNA strands, we need more than roster method or set builder descriptions.
Definition The set of nonnegative integers \(\mathbb{N}\) is defined (recursively) by: \[\begin{array}{ll} \textrm{Basis Step: } & \phantom{0 \in \mathbb{N}} \\ \textrm{Recursive Step: } & \phantom{\textrm{If } n \in \mathbb{N} \textrm{, then } n+1 \in \mathbb{N}} \end{array}\]
Examples:
Definition The set of all integers \(\mathbb{Z}\) is defined (recursively) by: \[\begin{array}{ll} \textrm{Basis Step: } & \phantom{0 \in \mathbb{Z}} \\ \textrm{Recursive Step: } & \phantom{\textrm{If } x \in \mathbb{Z} \textrm{, then } x+1 \in \mathbb{Z} \textrm{ and } x-1 \in \mathbb{Z}} \end{array}\]
Examples:
Definition The set of RNA strands \(S\) is defined (recursively) by: \[\begin{array}{ll} \textrm{Basis Step: } & \texttt{A}\in S, \texttt{C}\in S, \texttt{U}\in S, \texttt{G}\in S \\ \textrm{Recursive Step: } & \textrm{If } s \in S\textrm{ and }b \in B \textrm{, then }sb \in S \end{array}\] where \(sb\) is string concatenation.
Examples:
Definition The set of bitstrings (strings of 0s and 1s) is defined (recursively) by: \[\begin{array}{ll} \textrm{Basis Step: } & \phantom{\lambda \in X} \\ \textrm{Recursive Step: } & \phantom{\textrm{If } s \in X \textrm{, then } s0 \in X \text{ and } s1 \in X} \end{array}\]
Notation: We call the set of bitstrings \(\{0,1\}^*\) and we say this is the set of all strings over \(\{0,1\}\).
Examples:
Convert \((2A)_{16}\) to
binary (base )
decimal (base )
octal (base )
ternary (base )