2
| Inputs | Output | |
| \(x\) | \(y\) | \(x \text{ AND } y\) |
| \(1\) | \(1\) | \(1\) |
| \(1\) | \(0\) | \(0\) |
| \(0\) | \(1\) | \(0\) |
| \(0\) | \(0\) | \(0\) |

Fixed-width addition: adding one bit at time, using the usual column-by-column and carry arithmetic, and dropping the carry from the leftmost column so the result is the same width as the summands. Does this give the right value for the sum?
2 \[\begin{align*} & [0~ 1~ 0~ 1]_{s,4}\\ + & [1~ 1~ 0~ 1]_{s,4}\\ &\overline{\phantom{[0~0~1~0]_{s,4}}}\\ \end{align*}\]
\[\begin{align*} & [0~ 1~ 0~ 1]_{2c,4}\\ + & [1~ 0~ 1~ 1]_{2c,4}\\ &\overline{\phantom{[0~0~0~0]_{2c,4}}}\\ \end{align*}\]
3 \[\begin{align*} & (1~ 1~ 0~ 1~ 0~ 0)_{2,6}\\ + & (0~ 0~ 0~ 1~ 0~ 1)_{2,6}\\ &\overline{\phantom{(1~1~1~0~0~1)_{2,6}}}\\ \end{align*}\]
\[\begin{align*} & [1~ 1~ 0~ 1~ 0~ 0]_{s,6}\\ + & [0~ 0~ 0~ 1~ 0~ 1]_{s,6}\\ &\overline{\phantom{(1~1~1~0~0~1)_2}}\\ \end{align*}\]
\[\begin{align*} & [1~ 1~ 0~ 1~ 0~ 0]_{2c,6}\\ + & [0~ 0~ 0~ 1~ 0~ 1]_{2c,6}\\ &\overline{\phantom{(1~1~1~0~0~1)_2}}\\ \end{align*}\]
In a combinatorial circuit (also known as a logic circuit), we have logic gates connected by wires. The inputs to the circuits are the values set on the input wires: possible values are 0 (low) or 1 (high). The values flow along the wires from left to right. A wire may be split into two or more wires, indicated with a filled-in circle (representing solder). Values stay the same along a wire. When one or more wires flow into a gate, the output value of that gate is computed from the input values based on the gate’s definition table. Outputs of gates may become inputs to other gates.
2
| Inputs | Output | |
| \(x\) | \(y\) | \(x \text{ AND } y\) |
| \(1\) | \(1\) | \(1\) |
| \(1\) | \(0\) | \(0\) |
| \(0\) | \(1\) | \(0\) |
| \(0\) | \(0\) | \(0\) |

2
| Inputs | Output | |
| \(x\) | \(y\) | \(x \text{ XOR } y\) |
| \(1\) | \(1\) | \(0\) |
| \(1\) | \(0\) | \(1\) |
| \(0\) | \(1\) | \(1\) |
| \(0\) | \(0\) | \(0\) |
2
| Input | Output |
| \(x\) | \(\text{NOT } x\) |
| \(1\) | \(0\) |
| \(0\) | \(1\) |
Example digital circuit:
2
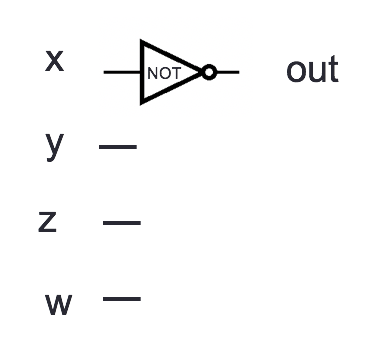
Output when \(x=1, y=0, z=0, w = 1\) is Output when \(x=1, y=1, z=1, w = 1\) is Output when \(x=0, y=0, z=0, w = 1\) is
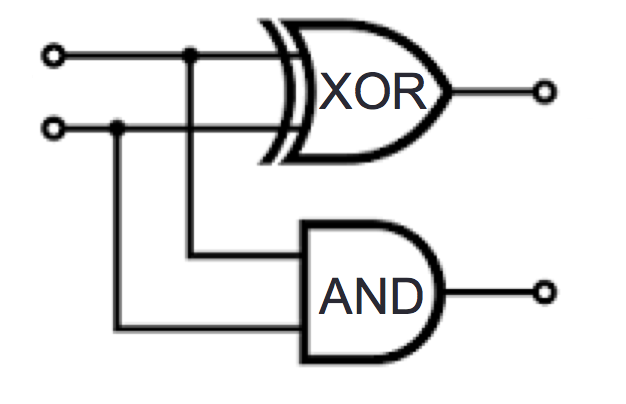
Draw a logic circuit with inputs \(x\) and \(y\) whose output is always \(0\). Can you use exactly 1 gate?
Fixed-width addition: adding one bit at time, using the usual column-by-column and carry arithmetic, and dropping the carry from the leftmost column so the result is the same width as the summands. In many cases, this gives representation of the correct value for the sum when we interpret the summands in fixed-width binary or in 2s complement.
For single column:
2
| Input | Output | ||
| \(x_0\) | \(y_0\) | \(c_0\) | \(s_0\) |
| \(1\) | \(1\) | ||
| \(1\) | \(0\) | ||
| \(0\) | \(1\) | ||
| \(0\) | \(0\) | ||
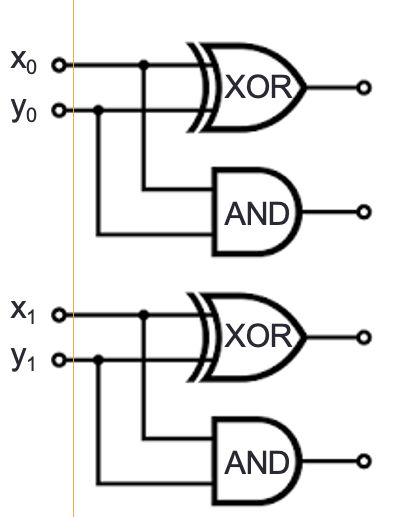
Draw a logic circuit that implements binary addition of two numbers that are each represented in fixed-width binary:
Inputs \(x_0, y_0, x_1, y_1\) represent \((x_1 x_0)_{2,2}\) and \((y_1 y_0)_{2,2}\)
Outputs \(z_0, z_1, z_2\) represent \((z_2 z_1 z_0)_{2,3} = (x_1 x_0)_{2,2} + (y_1 y_0)_{2,2}\) (may require up to width \(3\))
First approach: half-adder for each column, then combine carry from right column with sum of left column
Write expressions for the circuit output values in terms of input values:
\(z_0 = \underline{\phantom{x_0 \oplus y_0\hspace{3in}}}\)
\(z_1 = \underline{\phantom{(x_1 \oplus y_1) \oplus c_0}\hspace{2.5in}}\)
\(z_2 = \underline{\phantom{(c_0 \land (x_1
\oplus y_1)) \oplus c_1}\hspace{2in}}\)
There are other approaches, for example: for middle column, first add carry from right column to \(x_1\), then add result to \(y_1\)
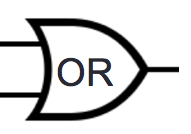
Truth tables: Input-output tables where we use \(T\) for \(1\) and \(F\) for \(0\).
| Input | Output | |||
| Conjunction | Exclusive or | Disjunction | ||
| \(p\) | \(q\) | \(p \land q\) | \(p \oplus q\) | \(p \lor q\) |
| \(T\) | \(T\) | \(T\) | \(F\) | \(T\) |
| \(T\) | \(F\) | \(F\) | \(T\) | \(T\) |
| \(F\) | \(T\) | \(F\) | \(T\) | \(T\) |
| \(F\) | \(F\) | \(F\) | \(F\) | \(F\) |
 |
 |
 |
||
| Input | Output |
| Negation | |
| \(p\) | \(\lnot p\) |
| \(T\) | \(F\) |
| \(F\) | \(T\) |
 |