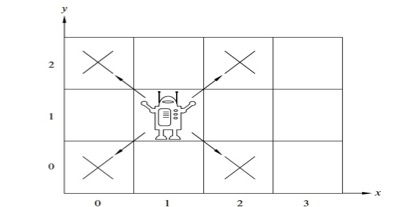

Theorem: A robot on an infinite 2-dimensional integer grid starts at \((0,0)\) and at each step moves to diagonally adjacent grid point. This robot can / cannot (circle one) reach \((1,0)\).
Definition The set of positions the robot can visit \(Pos\) is defined by: \[\begin{array}{ll} \textrm{Basis Step: } & (0,0) \in Pos \\ \textrm{Recursive Step: } & \textrm{If } (x,y) \in Pos \textrm{, then } \\ &\phantom{(x+1, y+1), (x+1, y-1), (x-1, y-1), (x-1, y+1)} \textrm{ are also in } Pos \end{array}\]
Example elements of \(Pos\) are:
Lemma: \(\forall (x,y) \in Pos~~( x+y \textrm{ is an even integer}~)\)
Why are we calling this a lemma?
Proof of theorem using lemma: To show is \((1,0) \notin Pos\). Rewriting the lemma to explicitly restrict the domain of the universal, we have \(\forall (x,y) ~(~ (x,y) \in Pos~~ \to ~~(x+y \textrm{ is an even integer})~)\). Since the universal is true, \((~ (1,0) \in Pos~~ \to ~~(1+0 \textrm{ is an even integer})~)\) is a true statement. Evaluating the conclusion of this conditional statement: By definition of long division, since \(1 = 0 \cdot 2 + 1\) (where \(0 \in \mathbb{Z}\) and \(1 \in \mathbb{Z}\) and \(0 \leq 1 < 2\) mean that \(0\) is the quotient and \(1\) is the remainder), \(1 ~\textrm{\bf mod}~ 2 = 1\) which is not \(0\) so the conclusion is false. A true conditional with a false conclusion must have a false hypothesis: \((1,0) \notin Pos\), QED. \(\square\)
Proof of lemma by structural induction:
Basis Step:
Recursive Step: Consider arbitrary \((x,y) \in Pos\). To show is: \[(x+y \text{ is an even integer}) \to (\text{sum of coordinates of next position is even integer})\] Assume as the induction hypothesis, IH that:
Theorem: Every positive integer greater than 1 is a product of (one or more) primes.
Before we prove, let’s try some examples:
\(20 =\)
\(100 =\)
\(5 =\)
Proof by strong induction, with \(b=2\) and \(j=0\).
Basis step: WTS property is true about \(2\).
Since \(2\) is itself prime, it is already written as a product of (one) prime.
Recursive step: Consider an arbitrary integer \(n \geq 2\). Assume (as the strong induction hypothesis, IH) that the property is true about each of \(2, \ldots, n\). WTS that the property is true about \(n+1\): We want to show that \(n+1\) can be written as a product of primes. Notice that \(n+1\) is itself prime or it is composite.
Case 1: assume \(n+1\) is prime and then immediately it is written as a product of (one) prime so we are done.
Case 2: assume that \(n+1\) is composite so there are integers \(x\) and \(y\) where \(n+1 = xy\) and each of them is between \(2\) and \(n\) (inclusive). Therefore, the induction hypothesis applies to each of \(x\) and \(y\) so each of these factors of \(n+1\) can be written as a product of primes. Multiplying these products together, we get a product of primes that gives \(n+1\), as required.
Since both cases give the necessary conclusion, the proof by cases for the recursive step is complete.
Suppose we had postage stamps worth \(5\) cents and \(3\) cents. Which number of cents can we form using these stamps? In other words, which postage can we pay?
\(11\)?
\(15\)?
\(4\)?
\[\begin{align*} &CanPay(0) \land \lnot CanPay(1) \land \lnot CanPay(2) \land \\ &CanPay(3) \land \lnot CanPay(4) \land CanPay(5) \land CanPay(6) \\ &\lnot CanPay(7) \land \forall n \in \mathbb{Z}^{\geq 8} CanPay(n) \end{align*}\]
where the predicate \(CanPay\) with domain \(\mathbb{N}\) is \[CanPay(n) = \exists x \in \mathbb{N} \exists y \in \mathbb{N} ( 5x+3y = n)\]
Proof (idea): First, explicitly give witnesses or general arguments for postages between \(0\) and \(7\). To prove the universal claim, we can use mathematical induction or strong induction.
Approach 1, mathematical induction: if we have stamps that add up to \(n\) cents, need to use them (and others) to give \(n+1\) cents. How do we get \(1\) cent with just \(3\)-cent and \(5\)-cent stamps?
Either take away a \(5\)-cent stamps and add two \(3\)-cent stamps,
or take away three \(3\)-cent stamps and add two \(5\)-cent stamps.
The details of this proof by mathematical induction are making sure we have enough stamps to use one of these approaches.
Approach 2, strong induction: assuming we know how to make postage for all smaller values (greater than or equal to \(8\)), when we need to make \(n+1\) cents, add one \(3\) cent stamp to however we make \((n+1) - 3\) cents.
The details of this proof by strong induction are making sure we stay in the domain of the universal when applying the induction hypothesis.
Consider the following game: two players start with two (equal) piles of jellybeans in front of them. They take turns removing any positive integer number of jellybeans at a time from one of two piles in front of them in turns.
The player who removes the last jellybean wins the game.
Which player (if any) has a strategy to guarantee to win the game?
Try out some games, starting with \(1\) jellybean in each pile, then \(2\) jellybeans in each pile, then \(3\) jellybeans in each pile. Who wins in each game?
Notice that reasoning about the strategy for the \(1\) jellybean game is easier than about the strategy for the \(2\) jellybean game.
Formulate a winning strategy by working to transform the game to a simpler one we know we can win.
Player 2’s Strategy: Take the same number of jellybeans that Player 1 did, but from the opposite pile.
Why is this a good idea: If Player 2 plays this strategy, at the next turn Player 1 faces a game with the same setup as the original, just with fewer jellybeans in the two piles. Then Player 2 can keep playing this strategy to win.
Claim: Player 2’s strategy guarantees they will win the game.
Proof: By strong induction, we will prove that for all positive integers \(n\), Player 2’s strategy guarantees a win in the game that starts with \(n\) jellybeans in each pile.
Basis step: WTS Player 2’s strategy guarantees a win when each pile starts with \(1\) jellybean.
In this case, Player 1 has to take the jellybean from one of the piles (because they can’t take from both piles at once). Following the strategy, Player 2 takes the jellybean from the other pile, and wins because this is the last jellybean.
Recursive step: Let \(n\) be a positive integer. As the strong induction hypothesis, assume that Player 2’s strategy guarantees a win in the games where there are \(1, 2, \ldots, n\) many jellybeans in each pile at the start of the game.
WTS that Player 2’s strategy guarantees a win in the game where there are \(n+1\) in the jellybeans in each pile at the start of the game.
In this game, the first move has Player 1 take some number, call it \(c\) (where \(1 \leq c \leq n+1\)), of jellybeans from one of the piles. Playing according to their strategy, Player 2 then takes the same number of jellybeans from the other pile.
Notice that \((c = n+1) \lor (c \leq n)\).
Case 1: Assume \(c = n+1\), then in their first move, Player 2 wins because they take all of the second pile, which includes the last jellybean.
Case 2: Assume \(c \leq n\). Then after Player 2’s first move, the two piles have an equal number of jellybeans. The number of jellybeans in each pile is \[(n+1) - c\] and, since \(1 \leq c \leq n\), this number is between \(1\) and \(n\). Thus, at this stage of the game, the game appears identical to a new game where the two piles have an equal number of jellybeans between \(1\) and \(n\). Thus, the strong induction hypothesis applies, and Player 2’s strategy guarantees they win.